Calibrating pH sensors is important for making accurate measurements. Almost all of these sensors use a glass junction electrode, which produces a voltage proportional to pH. For more info on how this works, check out our article on the subject.
A typical relationship between voltage and pH looks like this. Why did we put voltage on the x axis? We break down a measurement into 3 steps: #1: Create a model using calibration points. #2: Read voltage from the sensor. #3: Use our model to find the pH the voltage points to.
Why do we need to calibrate? Over time, sensors drift. This mean that the voltage they output for a given pH changes over time. Fortunately, this change is usually slow, and can be compensated for. How often you should calibrate depends on how much your sensor drifts (Higher quality sensors usually drift less), and how precise your measurements need to be. For example, for laboratory measurements, calibration should be done prior to each set of measurements. For hydroponic or aquarium use, once a month, or less frequently may work. You should test your sensor in a buffer of known pH once in a while, and check if the reading is close to what it should be. If you notice it's too far off, it's time to calibrate - you'll get a feel for how often you need to do it.
There are 2 main ways to calibrate. The main difference is whether we use 2, or 3 calibration points. In both, we measure voltage from the sensor while it's in a solution of known pH. The solutions are usually pH buffers, and can be bought online, or from laboratory suppliers. They are at a known pH, and resist changes to pH.
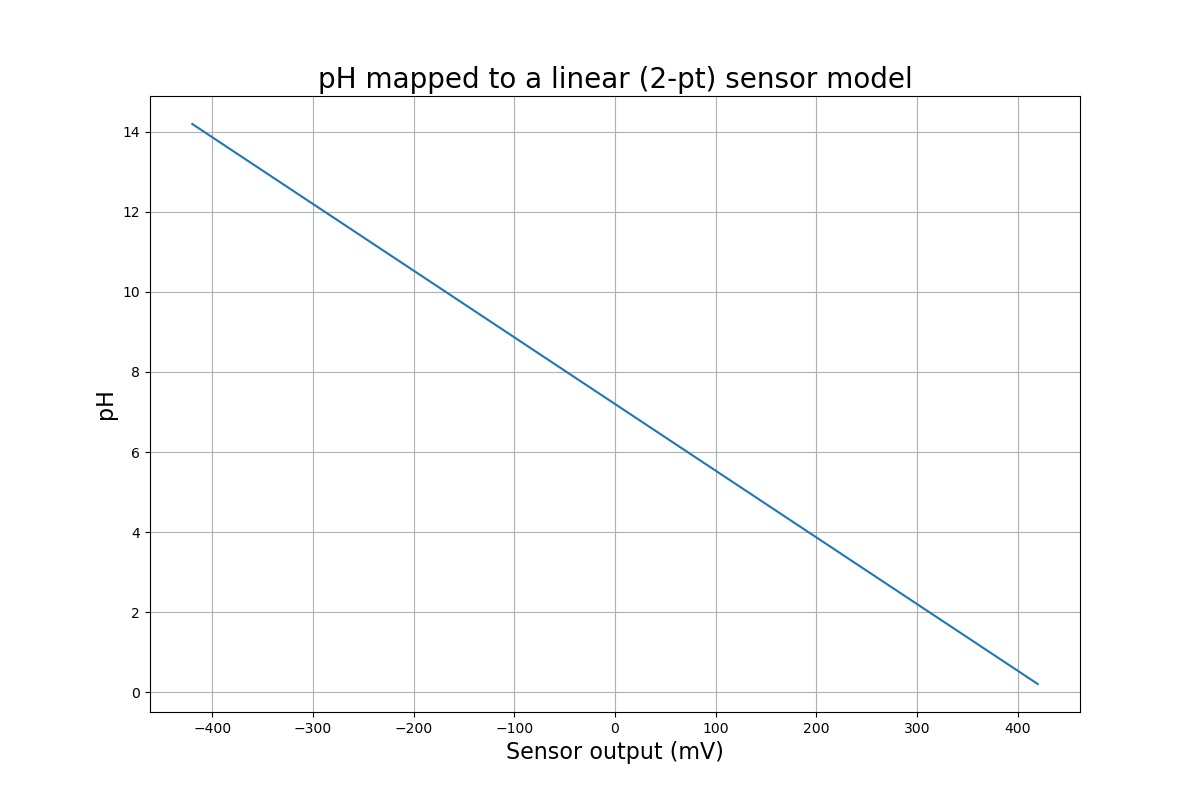
A linear model is a good approximation, and is good enough for most non-lab applications. It's also good enough if you know the pH being measured is in a narrow range, and you pick calibration points surrounding it. Here's all we need to know to calculate pH:
That's it. No arbitrary constants, and a simple formula. One way to represent a line as an equation is this, which you may remember from math class:
$$ pH = A \times x + pH_0 $$
We need to find the slope, \(A\), and the y-intercept, \(pH_0\), using our 2 calibration points. We start by calculating the slope, using the familiar rise-over-run formula:
$$ A = \frac{pH_2 - pH_1}{V_2 - V_1} $$
We're now ready to find the y-intercept: the pH where the sensor measures 0 Volts. This will be close to 7, but may vary on either side, depending on the sensor. We can use either calibration point for this:
$$ pH_0 = pH_1 - A \times V_1 $$
After placing these values in the first equation, we can find pH for any voltage from the sensor.
For the most accurate measurements, we need to model pH response as a curve - taking into account the slight non-linearity. There are a few ways to do this, but one that makes it easy is a Lagrange Polynomial. You might notice from that article that you're not limited to 3 points - you can use as many as you like! But 3's a good number, since it's more than accurate enough, and you might only have 3 buffers available.
An example, demonstrating a non-linearity in the sensor:
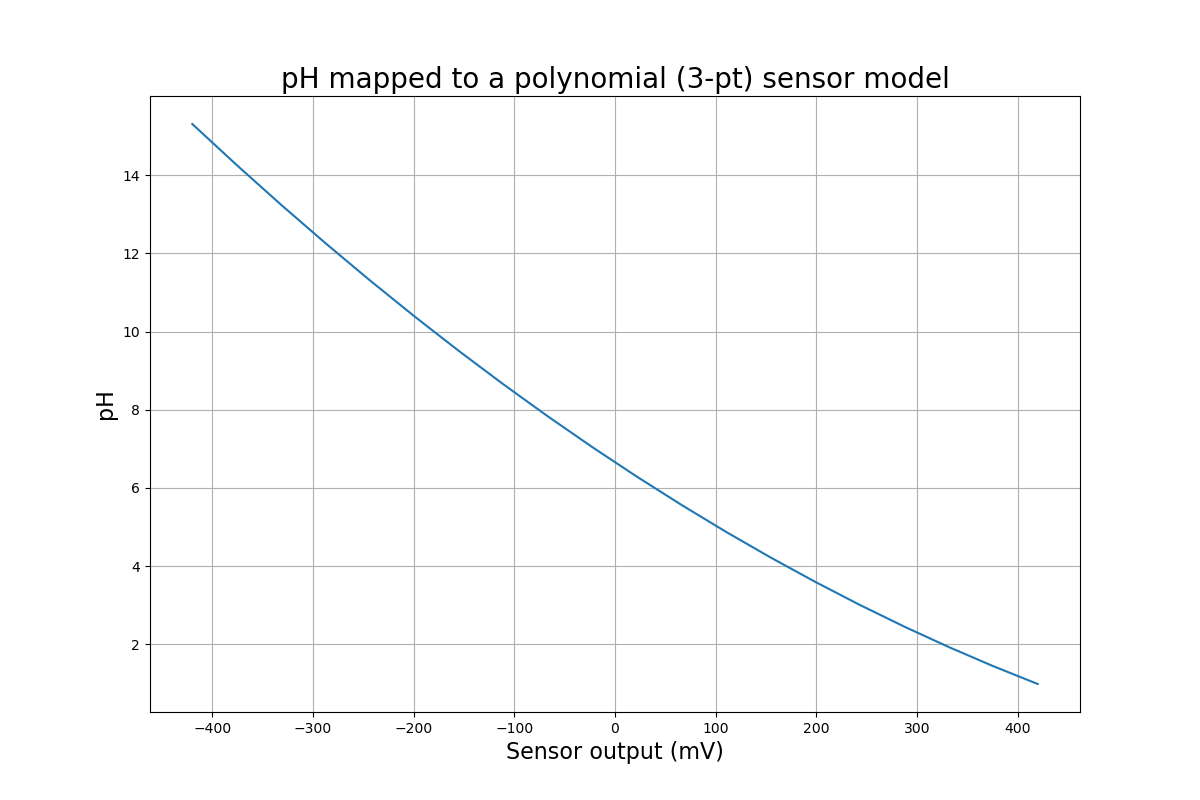
There are a few ways to mathematically write the formula for this polynomial. In code, it can be set up in a few lines using a nested loop.
If you pick your calibration points surrounding the expected value, and they're close together, the line, and curve models are very similar!
Check out the AnyLeaf ph driver on Github for an example of how to implement this with code.
If the measurement and calibration are done at significantly different temperatures, we need to change our model's slope to compensate. This is small change, unless the temperature difference is large. We could use a constant for this, for example, in our linear model, we'll use the constant \(T_{coeff} = -0.057 \frac{pH}{V \times T}\). \(V\) is in volts, and \(T\) is in °C. Then our formula becomes:
$$ pH = A\times T_{coeff} \times T_{diff} \times V + pH_0 $$
Where \(T_{diff}\) is the difference in temperature between calibration and measurement. Figure 2 of this paper from Texas Instruments shows how the slope changes with temperature.
Which method you use will depend on how accurate your measurements need to be, how much you expect them to vary, and the calibration methods provided by your sensor. If you're using a benchtop or handheld pH meter, or a microcontroller that outputs pH directly, you may be constrained to whatever options it has available. If you're using a sensor where you have access to the voltage, you can use whatever approach you'd like.
It's likely your device will let you initiate calibration with a button, menu, or digital command. Then, prompt you to place the sensor in a buffer solution (Either letting you specify the solution's pH, or requiring a specific buffer pH. It will measure the voltage and temperature, and store this calibration point (Buffer pH, voltage, temperature) somewhere, then repeat 1 or 2 more times, for 2 and 3-point calibration respectively.